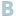中學校에 入學해서 代數를 배우기 시작한지 얼마 안될때 몇몇 친구들과 X2=X 2X=X의 方程式을 놓고 그것이 옳다 그르다 하고 떠들석했던 일이 생각난다. 그때 어떠한 結論이 내려져서 結末이 났는지는 기억이 없으나 當時의 氣分은 매우 純眞하고 素朴하였으며 그 態度는 퍽 率直했을 것이라는 것은 疑心이 가지 않는다. 우리의 常識的인 印象으로서는 어느 數가 그것을 自乘한 것 또는 그것을 몇곱한 것과 같다라는 것은 좀처럼 納得이 가지 않는다. 우리의 日常生活에서의 經驗은 그 自身의 自乘 數 또는 그 몇 倍의 數에 同一할 수 있는 數가 잇을 수가 있겟는가 하는 疑問을 불어이르키는 것이다. 이것은 우리가 普通 어느 數는 그것을 自乘 또는 몇 倍를 한 數에 比해서 恒常 적다고 생각하고 이러한 생각에 대해서 別로 疑心을 가져본 일도 없으며 또 이와같은 數에 대한 觀念을 前提로 하고 日常生活을 營爲하는데 何等의 障碍를 받아본 일이 없기 때문이라고 할 수 있다.

그러므로 어느 누군가가 위와같은 方程式에 對해서 그것은 훌륭히 成立되는 「참」된 것이라고 主張을 한다며는 우리는 자칫 잘못하다가는 그 主張의 옳고 그릇됨을 생각해 보려고도 하지 않고 그 사람의 數學에 關한 知識을 疑心하려고 하기 쉽다. 그러나 어느 數 x의 數値를 「1」로 하며는 그것의 自乘은 「1」이 되고 또 X의 數値를 「0」으로 하며는 그것을 몇 倍 모아도 「0」이 되므로 X의 數値를 「1」 또는 「0」으로 하는 限 위의 方程式은 「참」된 것으로 成立하게 된다. 그러나 만약 x가 「1」 또는 「0」 以外의 數値를 取하게 되면 위 各方程式의 成立은 「거짓」(僞)이 될 것이다. 그러므로 위 各方程式의 成立이 옳다고 하더라도 그것은 어디까지나 x의 數値가 「1」 또는 「0」인 境遇에 그것을 前提로 하는 限에서의 일이고 또 그것이 그릇된 것이라고 하더라도 그것은 x의 數値가 「1」또는 「0」 外의 것이라는 것을 前提로 하는 限에서의 論이 아닐 수 없는 것이다.

따라서 위의 論議는 그 前提로서 x의 數値를 어떻게 定하여야 할 것인가의 問題를 內包하고 있는 것이라고 하여야 할 것이다. 이와같은 前提가 되는 문제를 解決하지 않고 바로 該問題의 옳고 그르다는 것을 決定지우려는 것은 無意味한 노릇이 아닐 수 없다. 果然 그렇다면 위의 方程式의 成立에 대한 옳고 그르다는 主張은 그 모두가 「거짓」 主張은 아니지만 그 主張의 方式이 適切한 것이라고는 할 수 없다고 하여야 할 것이다. 왜냐하며는 그것을 「참」이라고 主張하려면 그 主張은 그 前提로서 x의 數値가 「1」 또는 「0」의 境遇에 限한다는 것이 그 主張의 脈絡에서 엿보일 수 있는 方式에 의하여야 할 것이고 또 그와같은 主張이 「거짓」 이라고 論駁하려며는 우선 該主張은 그 前提로서 x의 數値를 「1」또는 「0」으로 하는 것이 아니다라는 点이 論證되는 方式을 取하지 않으면 안되기 때문이다.

우리는 요즈음 위와같이 우선 解決하여야 할 前提問題를 명확히 함이 없이 덮어놓고 論題에 대함으로써 混亂을 招來하는 경우가 많다.

그리고 自己主張을 明確히 할 수 있는 方式을 取하지 못함으로써 意外의 誤解를 받게되는 境遇도 많다.

어느 主張을 할때에 그의 참뜻이 明確하게 上帶枋에게 傳達도리 수 있도록 그 表現方式에 特別한 留意를 하여야 할 것은 勿論이거니와 上帶枋의 主張에 對해서도 그 참뜻을 正確히 把握할 수 있도록 恒時 그 意見을 尊重하고 겸虛하게 그를 對하여야 하겠지만 이 바쁜 社會에서는 무엇보다도 相互間의 意見을 簡明하고 正確하게 그리고 알기쉽게 交換할 수 잇도록 그의 適切한 方法에 對한 特別한 硏究가 아쉽기만 하다.